前言
向被惠子老师发卡的阿光致敬
问题描述
- 场上站着3只精灵龙
- 我方手上一发复仇之怒
问题来了,复仇之怒打死1只,2只,3只精灵龙的概率
问题分析
还是用穷举的方法去解决这个问题,不过因为概率空间比较大,我们编程实现。
思路
我们用0,1,2,3分别表示对方英雄,以及三只精灵龙,那么概率空间中的元素可以表示成一个1x8的向量。
例如:[0,1,2,3,3,2,0,0]表示8发复仇之怒分别打中0(英雄),1(第一只精灵龙),2(第二只精灵龙),… ,0(英雄)
那么这个离散概率空间的概率分布是什么呢,或者说每一个基础元素的概率是多少呢?
为了解决这个问题,我们引入马尔科夫链,为了叙述(画图)方便,我们就用这个图来讲述一下概率分布。
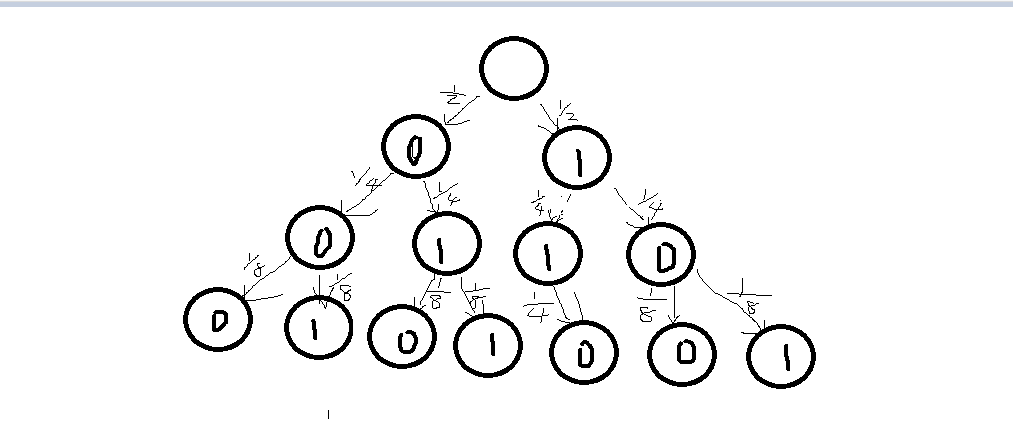
上图为问题《一只奥数飞弹打死一只精灵龙》的马尔科夫链
- 最上层的一个节点为root,概率为1.(代表所有概率空间的概率)
- 第二层表示第一发飞弹的概率分布,为一个均匀的伯努利分布,即1/2的概率打到英雄,1/2的概率打到精灵龙,这样概率就传递下来
- 第三层表示第二发飞弹的概率分布,我们知道第二发飞弹基于第一法飞弹的条件概率分布为一个均匀的伯努利分布,所以第二发飞弹的概率分布即为图种所示的4个概率为1/4节点。
- 第四层表示第三发飞弹的概率分布,和第二发类似,但是有一个重要区别:当前两发飞弹都打中精灵龙时,第三发飞弹只能打脸。
- 马尔可夫链中所有的叶子节点即为概率空间的元素。每个叶子节点的概率由马尔可夫链传递下来。
- 精灵龙被消灭这个事件的概率即为所有(精灵龙被消灭的)叶子节点的概率和(1/8 + 1/8 + 1/4)
同样类似,对于本文中的问题
- 最上层的一个节点为root,概率为1.(代表所有概率空间的概率)
- 每一个父节点拥有4个子节点(0,1,2,3),因为飞弹有4总选择可能
- 单出现一只精灵龙死亡的情况是,比如精灵龙1死亡,那么一个父节点只有3个子节点(0,2,3),并依此类推
- 一共有9层马尔可夫链(因为我们有8发飞弹么)
- 9层马尔科夫链的所有叶子节点即为所有的元素,他们的概率由马尔科夫链概率传导可得。
- 精灵龙被消灭这个事件的概率可由所有对应叶子节点的和来计算。