问题背景
玩炉石的朋友经常会遇到这种情况:
- 对方场上只站着一只精灵龙
- 我方手中只有一发奥数飞弹
这时候,问题来了:要不要用奥术飞弹呢,奥数飞弹解掉精灵龙的概率是多少呢?
分析问题
这个其实是一个概率论的问题。
我们知道3发奥数飞弹全打脸的概率是1/8=(1/2 x 1/2 x 1/2),那3发奥数飞弹打死一个2血的精灵龙的概率是多少呢。
这个问题其实我们可以用穷举法表示,我们用[1,0,1]来表示第一法打中精灵龙,第二发打中英雄,第三发打中精灵龙。那么所有情形我们可以写出来:
- [0,0,0] — 1/8 — a1
- [0,0,1] — 1/8 — a2
- [0,1,0] — 1/8 — a3
- [1,0,0] — 1/8 — a4
- [0,1,1] — 1/8 — a5
- [1,0,1] — 1/8 — a6
- [1,1,0] — 1/4 — a7
- [1,1,1] — 0 — a8
我们发现其实[1,1,1]是不存在的,因为精灵龙中了2发奥数飞弹就被消灭了,不可能中3发,所以他的概率是0.而[1,1,0]的概率为什么是1/4呢,因为前两发打中精灵龙后,最后一发必打脸,所以概率是1/4=(1/2 x 1/2 x 1),所以我们发现精灵龙被消灭的概率是所有打中精灵龙2发奥数飞弹的情况,即1/8 + 1/8 + 1/4 = 1/2
这是阿光智商的分割线,以下内容请勿看
抽象一下
为了解决更复杂的问题,我们介绍几个概率论的定义
- 概率空间Ω:所有元素的集合,如{a1,a2,a3,a4,a5,a6,a7}
- 事件F:Ω的一个子集,例如精灵龙被消灭{a5,a6,a7}
- 概率测度p:F->R是一个从事件F到[0,1]的概率函数。
那么本文的例子其实是求一个事件(精灵龙被消灭)对应的概率。
对于离散的的概率空间(Ω,F,P)而言,针对本文的情况,有一个很好的模型可以去解决这种问题:马尔可夫链
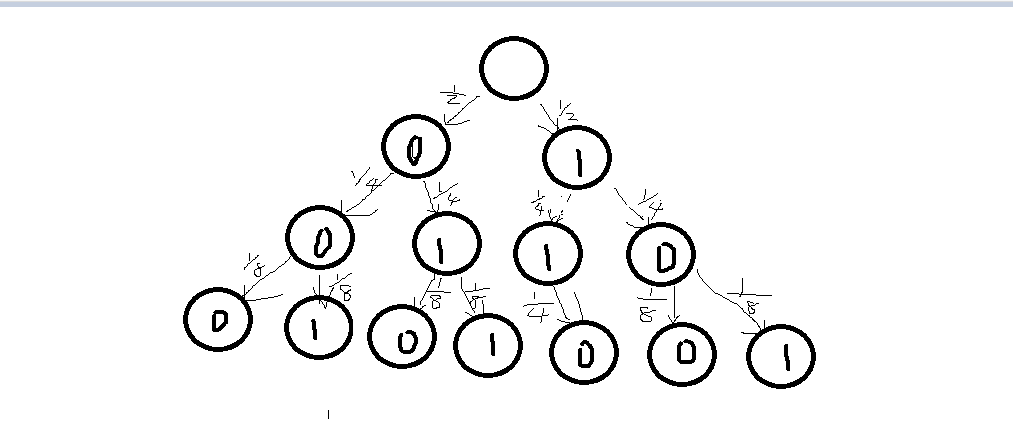
发现了么,其实我们可以用一个马尔科夫链表去刻画这个情形,所有叶子即概率空间的元素(从上到下的路径)
那么问题来了: 场上3只精灵龙,复仇之怒打死2只精灵龙的概率是多少?
预告
请听下回分解:马尔可夫链之九层妖塔。